
RESUMEN DEL TEMA 14 DEL TEMARIO OFICIAL DE LA ESPECIALIDAD DE MATEMÁTICAS DE SECUNDARIA
Esquema:
1. Ecuaciones.
1.1. Definiciones.
1.2. Relación entre los coeficientes y las raíces de
una ecuación.
1.3. Ecuaciones equivalentes.
1.4. Raíces complejas, racionales y enteras.
2. Resolución de ecuaciones.
3. Acotación de raíces reales.
4. Separación de raíces reales.
4.1. Regla de acotación de newton.
4.2. Regla de laguerre-thibault.
4.3. Método de sturm.
5. Aproximación numérica de raíces reales.
5.1. Método de horner.
5.2. Método de la regla-falsi (o de la falsa-posición).
5.3. Método de newton.
5.4. Método de iteración.
6. Referencias bibliográficas y documentales.
1. ECUACIONES.
1.1. DEFINICIONES.
Una ecuación algebraica es una expresión de la forma P(x) = axn + axn-1 + … = 0 donde P(x)ϵc[x] , es decir, P(x) es un polinomio de la variable compleja x cuyos coeficientes también son números complejos.
Los ceros de P(x) o raíces de la ecuación P(x) = 0 son los aϵc , tal que P(a) = 0.
El mayor número natural n tal que an ≠ 0 , se llama grado de la ecuación. Sobre las raíces de un polinomio, tenemos la siguiente propieda
Teorema del factor:
Demostración:
La existencia de raíces de una ecuación:
Viene dada por el teorema fundamental del Álgebra, que dice así: Todo polinomio, no constante, cuyos coeficientes son números complejos tiene, al menos, una raíz compleja. La demostración de este teorema, requiere recursos de la teoría de funciones de variable compleja que se salen fuera de los objetivos de este tema.
1.2. RELACIÓN ENTRE LOS COEFICIENTES Y LAS RAÍCES DE UNA ECUACIÓN.
Teorema: Sean a1, ….an ϵc las raíces , que pueden ser distintas o no, de una ecuación algebraica P(x) = axn + axn-1 + … = 0. Entonces se verifican las siguientes relaciones:
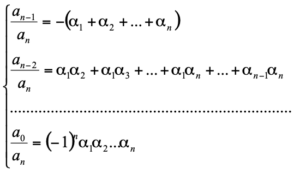
Observación: Estas relaciones son llamadas fórmulas de Cardano-Vieta, pues Jerónimo Cardano (1501-1576) conocía que la suma de las raíces de la ecuación es , y FrançoisViète (1540-1603), o en su forma latinizada, Franciscus Vieta, generalizó un poco estas relaciones.
1.3. ECUACIONES EQUIVALENTES.
Definición: Dos ecuaciones algebraicas son equivalentes, si tienen las mismas raíces con los mimos órdenes de multiplicidad.
Propiedad: La condición necesaria y suficiente para que dos ecuaciones algebraicas sean equivalentes es que sus respectivos coeficientes sean proporcionales.
Demostración:
1.4. RAÍCES COMPLEJAS, RACIONALES Y ENTERAS.
Una ecuación P(x) = 0 donde P(x)ϵIR[x] con coeficientes reales, puede tener raíces reales y/o complejas. A su vez las raíces reales pueden ser enteras, (negativas, cero, positivas), fraccionarias e irracionales. Ocupémonos de las raíces complejas, racionales y enteras.
Teorema 1: Si la ecuación P(x) = 0 con coeficientes reales admite una raíz compleja a + ib de orden k, entonces, su conjugado a – ib es también raíz de orden k.
Demostración: Sustituyendo x por a + ib en el polinomio P(X), resulta que las potencias pares de ib darán números reales y las impares darán múltiplo de i. Sea A la suma de todos los números reales que resultan de esa sustitución y Bi la suma de los múltiplos de i. Por tanto, al sustituir a + ib en P(X), la ecuación se reduce a P(a + ib) = A + Bi = 0 , lo que equivale
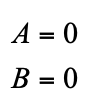
2. RESOLUCIÓN DE ECUACIONES.
A) Ecuación de primer grado:
B) Ecuación de segundo grado o ecuación cuadrática:
Un caso particular de ecuaciones de grado 4 que se pueden reducir a la resolución de una ecuación de grado2, son las siguientes:
Ecuaciones bicuadradas: Son ecuaciones de grado 4 de la forma
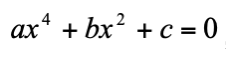
C) Ecuaciones cúbicas: La ecuación general de tercer grado, dividiendo ambos miembros por su primer coeficiente
3. ACOTACIÓN DE RAÍCES REALES.
Definición: Se dice que M ϵ IR es una cota superior de las raíces reales de una ecuación algebraica P(x)=0 si es mayor que cualquiera de dichas raíces y se dice que es una cota inferior si es menor que cualquiera de ellas.
Para acotar las raíces de una ecuación algebraica basta con dar reglas para determinar una cota superior.
4. SEPARACIÓN DE RAÍCES REALES.
Para acotar separadamente las raíces positivas y las raíces negativas, basta con obtener una regla para determinar una cota superior M de la raíces positivas de la ecuación P(x)=0. Así, ejecutando el mismo procedimiento con P(-x) se obtiene la cota inferior de las raíces negativas (Obteniendo la cota superior de las raíces positivas de P(-x) y cambiándolas de signo).
4.1 REGLA DE ACOTACIÓN DE NEWTON.
Demostración: Desarrollando el polinomio P(x) mediante el polinomio de Taylor de grado menor o igual que n de P en M, se tiene
![]()
Si x ≥ M entonces P(x)>0 por ser suma y producto de términos positivos, y por tanto, M es cota superior.
4.2. REGLA DE LAGUERRE-THIBAULT.
Si en la división de P(x) por x-M resulta que todos los coeficientes del cociente y también del resto son positivos, entonces M es una cota superior de las raíces de P(x)=0.
Demostración: Efectuando la división resulta
![]()
Si x ≥ M entonces P(x)>0 por ser suma y producto de términos positivos, y por tanto, M es cota superior.
4.3. MÉTODO DE STURM.
Sirve para contar el número de raíces de una ecuación con coeficientes reales que hay en un intervalo El método dice así: Sea P(X)=0 una ecuación con coeficientes reales de grado n, que supondremos que admite únicamente raíces simples (lo que no restinge generalidad, pues, toda ecuación con raíces múltiples se puede reducir a otra con raíces simples) y sea P’(X) su polinomio derivado.
5. APROXIMACIÓN NUMÉRICA DE RAÍCES REALES.
5.1. MÉTODO DE HORNER.
Supongamos que la ecuación
![]()
tiene una raíz s comprendida entre (a,a + 1) donde aϵz , es decir, comprendida en un intervalo abierto de extremos dos números enteros consecutivos. Podemos suponer que s>0, pues cuando se trate de encontrar alguna raíz negativa bastará buscar la correspondiente raíz positiva en la ecuación obtenida al cambiar x por –x. Así, resulta que aϵz es la parte entera de s.
5.2. MÉTODO DE LA REGLA-FALSI (O DE LA FALSA-POSICIÓN).
Sea f(x)=0 una ecuación (algebraica o transcendente) tal que tiene una única raíz s en (a,b) , f es continua en [a,b] y tal que f(a)·f(b)<0. La ecuación de la recta que pasa por (a,f(a)) y (a,f(b)) es:
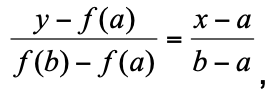
5.3. MÉTODO DE NEWTON.
A las hipótesis anteriores de que f(x)=0 es una ecuación (algebraica o transcendente) tal que tiene una única raíz s en (a,b) , f es continua en [a,b] y f(a)·f(b)<0, le añadimos que f sea derivable en (a,b) y que su derivada f´(x) mantiene el signo en (a,b) .
El método de Newton consiste en sustituir la curva y=f(x) por la tangente en uno de los extremos (a ó b) que designaremos por X0 , sin precisar, de momento, a cuál de los dos corresponde.
5.4. MÉTODO DE ITERACIÓN.
La ecuación propuesta puede venir dada de la forma x=g(x) de diversas maneras. Esta ecuación equivale a resolver f(x)=x-g(x)=0, de la cual sabemos que existe una raíz s en el intervalo [a,b] .
La idea central para resolver x=g(x) es tomar un punto Xo aproximado de s y formar la sucesión.
6. REFERENCIAS BIBLIOGRÁFICAS Y DOCUMENTALES.
- MARTÍNEZ SALAS, J. Elementos de matemáticas. Valladolid, 1969.
- REY PASTOR, J. Elementos de Análisis Algebraico. Madrid, 1958.
- REY PASTOR, J., PI CALLEJA , P., A. TREJO, C. Análisis matemático. Ed. Kapelusz. 1952.
- DIEUDONNÉ, J. Cálculo infinitesimal. Ed. Omega, S.A. 1971.


